数学で解き明かす速さの見方・考え方【面積図】

皆さん、こんにちは。
今回は、ものの見方や考え方について、「速度」の点からお話しします。
車や電車など、「速度」そのものは身近な存在だと思いますが、“こんな見方もできるんだ!”と新たな発見があるかもしれません。ぜひご覧ください。
【数学で解き明かす】40km/hと60km/hの平均速度は?
行きに40km/hで進んで、帰りに60km/hで戻ってきたときの平均速度って、おわかりになりますか?
「単純に考えて、(40km/h+60km/h)÷2=50km/hじゃないの?」と考える方が多いかと思います。
では、実際にそうなるか、検証してみましょう。

全体の距離が120kmだとします。別にこの距離は何kmでもいいのですが、40と60の共通の倍数としておくと計算がしやすいので、120kmにします。
すると、例えば、
行きは40km/h で120km進みました。かかった時間は3時間になります。
帰りは60km/h で同じく、120km進みました。時間は2時間になります。
これら両方の条件から、実際は240kmの距離を5時間かかるスピードで進んだことになります。
↓
240km÷5時間=48km/h
この式から、行きと帰りを合わせた速さは48km/hだったことがわかります。つまり、時速40kmと時速60kmの平均は、時速48kmだったということになります。
では、ほかの考え方はできないでしょうか?
こんな考え方はどうでしょう。
そもそも、時速とは「1時間あたりにどれくらいの距離(km)を進むことができるか」を表した速さの単位になります。
ちょっと考え方を捻ってみて、この時速の逆数を取ります。そうすると、どうなるでしょう。
これは、それぞれの速さに対して「1kmあたりの距離を進むのに何時間かかったか」になるのが、おわかりになりますか?式で表すと、こうなります。
40 の逆数は、1/40 です。
60 の逆数は、1/60 です。これの平均ですから、
(1/60+1/40)/2
になります。通分して、
(2/120+3/120)/2 = (5/120)/2 = 5/240
になります。
今、「1mあたりの距離を進むのに何時間かかったか」を計算したのですが、求めたいのは「1時間あたりにどれくらいの距離を進むことができるか」なので、これの逆数を取ります。
240/5=48
先ほど計算した、時速40km と 時速60km の平均である時速48kmと一致しましたね。
【数学で解き明かす】速度の問題に面積図を使った考え方
先程の計算は、面積図を使ってみるとどうでしょう。
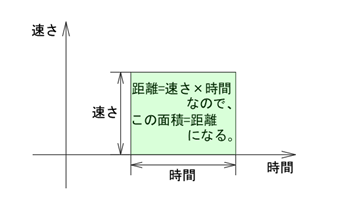
「時速=距離÷時間」は、かけ算に直すと「距離=速さ×時間」になります。
このかけ算を面積で表現しようという考え方です。
縦軸を「速さ」、横軸を「時間」とすることで、長方形の面積が「距離」を表すことになりますね。
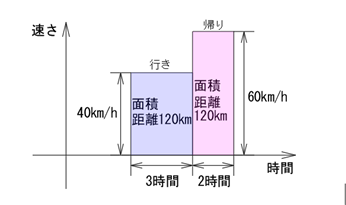
「平均の速さを出したい」ということは、「距離」である面積を変えずに「速さ」である縦軸を揃えたいということになります。これはつまり、下図2つの長方形をどう変形させたら等しくなるでしょう?という考え方になります。
「時間」である横軸は、5時間を半分にすればちょうど等しくなるので、2.5時間に変形することになります。そのとき、「距離」である面積を変えないまま、「速さ」である縦軸を変化させるには、どれだけ増減すればいいのでしょうか?
ここには、実はある法則があります。
元の長方形の底辺である横軸の「時間」の比が3:2だったことにお気づきでしょうか?
そのとき、縦軸である「速さ」を平均化させるための比は、その逆比である2:3になるのです。
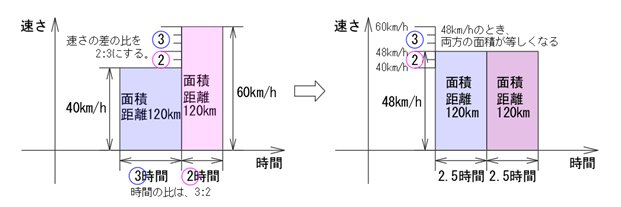
つまり、縦軸はこんな感じで変化させることになります。
時速40km 基準の場合
40+((60-40)×(2/5))
=40+(20×2/5)
=48時速60km 基準の場合
60-((60-40)*(3/5))
=60-(20*3/5)
=48
いずれにしても、時速40km と 時速60km の平均は、時速48kmと一致しました。
こんな風に、ひとつの物事を取っても、計算する方法はいくつも存在します。
いろいろな見方をすることで、いつもと違う考え方ができるかも知れません。
太陽光発電の計算でも、面積図は使用されています!
実は、太陽光発電においても、この面積図の考え方を使用しています。
それを「日負荷曲線」といいます。
この場合、縦軸に「電力(kW)」、横軸に「時間」を取ります。
すると、縦軸と横軸のかけ算が発電量(kWh)になるのです。
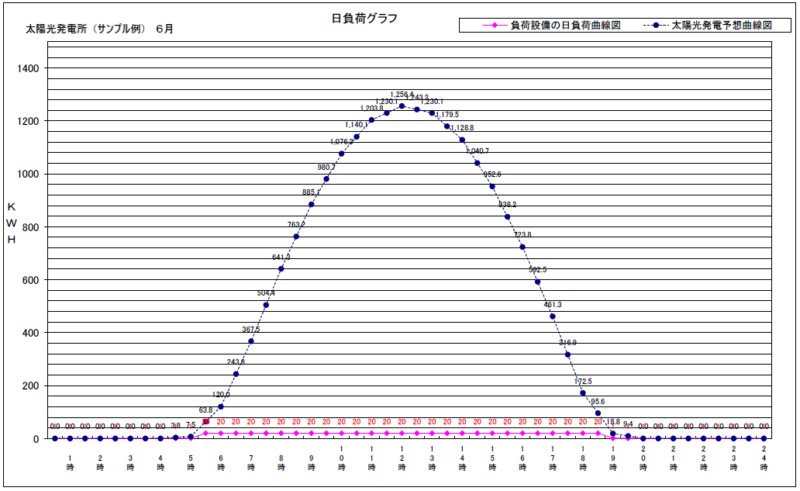
(太陽光発電所:日負荷曲線グラフ例)
これは、視覚的に発電量をわかりやすく把握するための工夫のひとつです。
――――✏―――✏―――✏――――
いかがでしたか?
当社は、大型の太陽光発電所や工場・屋上屋根への自家消費型太陽光発電、そして住宅用太陽光発電など、さまざまな案件の設計から施工までをおこなっています。
設計時には、今回のような視点やほかにも多角的な視点から、最適な形を検討しご提案しています。導入を考えている方は、ぜひ一度発電量シミュレーションだけでもご相談ください。
次回は「円の面積の求め方と考え方」について解説します。お楽しみに!
☞自家消費型太陽光発電の設計ポイントを詳しく知りたい方はコチラ
☞太陽光で今最も注目されている「FIP制度」をわかりやすく解説!
 ご相談・お問い合わせ
ご相談・お問い合わせ
ご相談希望の内容を下記より選択ください。(複数選択可)








